Công thức tính diện tích hình thang vuông

Hình thang là gì? công thức tính chu vi hình thang? công thức tính diện tích s hình thang? các dạng bài xích tập về hình thang? một vài bài tập về hình thang?

Hình thang là 1 hình học thông dụng và đơn giản trong Toán học. Đây là dạng hình rất thường được sử dụng trong các bài tập hình học nhất là các dạng toán nâng cao. Bài viết dưới đây vẫn tổng hợp tất cả kiến thức liên quan đến hình thang.

Bạn đang xem: Công thức tính diện tích hình thang vuông

1. Hình thang là gì?

1.1. Khái niệm:

Hình thang vào hình học tập Euclide là một tứ giác tất cả hai cạnh đối tuy vậy song. Hai cạnh tuy vậy song này được hotline là những cạnh lòng của hình thang, hai cạnh sót lại gọi là cạnh bên.

Hình thang là tứ giác có hai cạnh đối tuy nhiên song, nhị góc kề một ở bên cạnh có tổng bằng 180 độ.

Hình thang là tứ giác lồi gồm 4 cạnh. Trong các số ấy có hai cạnh tuy nhiên song với nhau được điện thoại tư vấn là cạnh đáy, nhì cạnh sót lại được điện thoại tư vấn là nhị cạnh bên.

Ngoài ra hình thang còn có một số trường hợp đặc trưng như:

– Hình thang vuông: Hình thang có một góc vuông được call là hình thang vuông

– Hình thang cân: Hình thang bao gồm 2 góc kề một cạnh đáy đều bằng nhau là hình thang cân.

– Hình thang vuông cân: Là hình thang vừa vuông vừa cân nặng và nói một cách khác là hình chữ nhật.

1.2. đặc thù của hình thang:

Tính hóa học về cạnh

– Hình thang có hai cạnh đáy đều nhau thì hai cạnh bên sẽ tuy nhiên song và bằng nhau.

– Hình thang gồm hai kề bên song song thì hai kề bên bằng nhau cùng hai cạnh đáy bởi nhau.

Đường trung bình của hình thang:

– Đường vừa phải của hình thang là đoạn trực tiếp nối trung điểm hai cạnh bên của hình thang

Tính chất: Đường trung bình của hình thang thì song song với hai lòng và bởi nửa tổng nhị đáy.

Tính hóa học về góc

– nhị góc kề một ở bên cạnh của hình thang gồm tổng bởi 180 độ ( hai hóc nằm ở trong phần trong thuộc của nhì đoạn thẳng tuy vậy song là nhị cạnh đáy) .

– vào hình thang cân, hai góc kề một đáy bởi nhau.

1.3. Dấu hiệu nhận biết:

Dấu hiệu nhận thấy hình thang đó là định nghĩa của hình thang hay: tứ giác có hai cạnh đối tuy nhiên song cùng với nhau.

Ví dụ: Tứ giác ABCD tất cả AB // CD ⇔ Tứ giác ABCD là hình thang.

Tổng hợp các dấu hiệu nhận biết hình thang là:

– Hình thang là hình tứ giác có hai cạnh đối tuy vậy song cùng với nhau.

– Tứ giác là hình thang gồm một góc vuông là hình thang vuông.

– Tứ giác là hình thang gồm hai góc kề 1 cạnh đáy đều nhau thì là hình thang cân.

– Tứ giác là hình thang bao gồm hai sát bên hình thang cân nhau thì là hình thang cân.

– Tứ giác là hình thang mà lại hai đường chéo của chúng cân nhau thì là hình thang cân.

Lưu ý: đối với dấu hiệu phân biệt hình thang cân nặng thì dễ dàng hơn:

– Hình thang tất cả hai góc kề một cạnh đáy bằng nhau là hình thang cân.

– Hình thang gồm hai đường chéo bằng nhau là hình thang cân.

– Hình thang bao gồm hai trục đối xứng của hai đáy trùng nhau là hình thang cân.

– Hình thang gồm hai kề bên bằng nhau là hình thang cân.

– Hình thang nội tiếp mặt đường tròn là hình thang cân

2. Cách làm tính chu vi hình thang:

Chu vi hình thang là độ lâu năm đường phủ quanh một hình thang. Trường đoản cú chu vi được dùng đối với cả hai tức là đường phủ quanh một diện tích hình thang và tổng độ lâu năm của đường này.

Công thức tính chu vi hình thang: Chu vi hình thang bởi tổng các lân cận và cạnh đáy.

P = a + b + c + d

Trong đó: p. Là chu vi hình thang,

a và b thứu tự là độ dài 2 cạnh đáy,

c và d lần lượt là độ nhiều năm 2 cạnh bên.

Ví dụ minh họa: Một hình thang tất cả độ lâu năm các ở bên cạnh lần lượt là 8cm, độ lâu năm đáy béo là 16 cm và độ lâu năm đáy bé xíu là 8 cm. Tính chu vi hình thang.

Xem thêm: Phần Mềm Tạo Virus Theo Ý Muốn !, Phần Mềm Tạo Virus Theo Ý Muốn

Bài giải:

Chu vi hình thang là:

8+8+8+16 = 40 (cm)

Đáp số chu vi của hình thang = 40 cm

3. Cách làm tính diện tích s hình thang:

Công thức tính diện tích s hình thang: trung bình cộng 2 cạnh đáy nhân với chiều cao giữa 2 đáy.

S = (a + b)/2 x h

Trong đó: S là diện tích hình thang.

a và b là độ nhiều năm 2 cạnh đáy.

h là chiều cao hạ từ bỏ cạnh đáy a xuống b hoặc trái lại (khoảng biện pháp giữa 2 cạnh đáy).

Còn có bài thơ về tính diện tích s hình thang khá dễ dàng nhớ như sau:

Muốn tính diện tích s hình thang

Đáy lớn đáy nhỏ ta đem cùng vào

Cộng vào nhân cùng với chiều cao

Chia đôi đem nửa thế nào thì cũng ra

Công thức tính diện tích hình thang khi biết 4 cạnh (bài toán nâng cao)

Hình thang cùng với chiều dài 4 cạnh

Trong trường hợp việc cho dữ khiếu nại biết độ lâu năm của 4 cạnh, nói rõ cạnh lòng a, c với cạnh lòng c to hơn cạnh lòng a, ở kề bên là b cùng d thì chúng ta có thể tính được diện tích hình thang theo công thức sau.

Công thức tính diện tích hình thang khi biết 4 cạnh

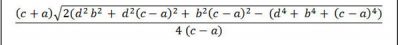
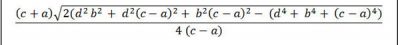
Trong đó: S: Diện tích

a: cạnh đáy bé

c: cạnh lòng lớn

b, d: kề bên hình thang

Cách tính diện tích hình thang vuông

Hình thang vuông là hình thang bao gồm một góc vuông. Kề bên vuông góc với hai lòng cũng đó là chiều cao h của hình thang.

Công thức tầm thường tính diện tích s hình thang vuông tương tự như hình thang thường: trung bình cùng 2 cạnh lòng nhân với độ cao giữa 2 đáy, tuy vậy chiều cao ở đó chính là ở kề bên vuông góc với tất cả 2 đáy.

S = (a + b)/2 x h

Trong đó: S là diện tích hình thang.

a cùng b là độ nhiều năm 2 cạnh đáy.

h là độ dài sát bên vuông góc với 2 đáy.

4. Các dạng bài bác tập về hình thang:

Dạng 1: Tính chu vi hình bình thang lúc viết độ dài những đáy với cạnh bên

Ví dụ: Tính chu vi của hình thang, biết đáy lớn bằng 12 cm; đáy bé bỏng bằng 10 cm và hai bên cạnh lần lượt bằng 7 centimet và 8 cm

Lời giải:

Chu vi hình thang là:

12 + 10 + 7 + 8 = 37 (cm)

Đáp số: 37cm

Dạng 2: Tính độ dài lân cận của hình thang cân khi biết chu vi

Ví dụ: Tính độ nhiều năm của hình thang có hai sát bên bằng nhau biết chu vi của hình thang bằng 68cm với độ nhiều năm hai cạnh đáy lần lượt là 20cm và 26cm.

Lời giải:

Tổng độ dài hai lân cận của hình thang là:

68 – 20 – 26 = 22 (cm)

Độ dài lân cận của hình thang là:

22 : 2 = 11 (cm)

Đáp số: 11cm

Dạng 3: Tính diện tích s hình bình thang khi biết độ dài hai đáy cùng chiều cao

Ví dụ: cho hình thang bao gồm độ lâu năm đáy nhỏ tuổi bằng 5cm, đáy lớn bởi 10cm. Chiều cao của hình thang bằng 6cm. Tính diện tích của hình thang đó.

Lời giải:

Diện tích hình thang là:

(5 + 10) x 6 : 2 = 45 (cm2)

Đáp số: 45cm2

Dạng 4: Tính độ cao khi biết độ nhiều năm hai đáy và ăn diện tích

Ví dụ: Một hình thang vuông có diện tích bằng 14dm2, đáy bé nhỏ bằng 2dm và đáy lớn bằng 5dm. Tính độ dài chiều cao của hình thang vuông đó.

Từ phương pháp tính diện tích s hình thang, ta suy ra được bí quyết tính độ cao của hình thang, kia là: h = S x 2 : (a + b) (Để tính độ cao của hình thang, ta lấy diện tích s chia đến trung bình cùng của hai đáy.)

Lời giải:

Độ dài độ cao của hình thang là:

14 x 2 : (2 + 5) = 4 (dm)

Đáp số: 4dm

Dạng 5: Tính diện tích s hình thang khi chưa chắc chắn độ dài hai đáy cùng chiều cao

Ví dụ 1: Một hình thang có chiều cao bằng 56cm. Đáy to hơn đáy bé bỏng 24cm và đáy bé bỏng bằng 2/5 đáy lớn. Tính diện tích hình thang.

Lời giải:

Hiệu số phần bằng nhau là:

5 – 2 = 3 (phần)

Độ lâu năm đáy béo là:

24 : 3 x 5 = 40 (cm)

Độ lâu năm đáy nhỏ xíu là:

40 – 24 = 16 (cm)

Diện tích hình thang là:

(16 + 40) x 56 : 2 = 1568 (cm2)

Đáp số: 1568cm2

5. Một số trong những bài tập về hình thang:

Bài 1: cho hình thang có hai cạnh lòng lần lượt là 6cm và 4cm. Chiều dài của cạnh bên bằng một phần hai tổng độ dài hai cạnh đáy. Tính chu vi của hình thang đó, biết rằng hình thang có hai sát bên bằng nhau?

Bài 2: Một hình thang bao gồm độ nhiều năm đáy lớn bằng 4,5dm; độ lâu năm đáy nhỏ bẳng 60cm và chiều cao bằng 8dm. Tính diện tích s của hình thang đó.

Bài 3: Có một mảnh đất nền hình thang với đáy bé bỏng là 24m, đáy bự là 30m. Không ngừng mở rộng hai dáy về phía bên yêu cầu của mảnh đất với đáy phệ thêm 7m, đáy nhỏ tuổi thêm 5m thu được mảnh đất hình thang new với diện tích lớn hơn diện tích ban đầu là 36m2. Tính diện tích s mảnh đất hình thang ban đầu.

BÀI 4: Tính diện tích s hình thang gồm đáy lớn bằng 50 dm và bằng 80% chiều cao, đáy nhỏ bé kém đáy mập 12 dm.

BÀI 5: Tính diện tích s hình thang có chiều cao bằng 4 dm, đáy bé nhỏ bằng 80% chiều cao và hèn đáy béo 1,2 dm.

BÀI 6: Hình thang bao gồm tổng độ lâu năm hai đáy bằng 24 cm, đáy to hơn đáy bé xíu 1,2 cm, độ cao kém đáy nhỏ bé 2,4 cm. Tính diện tích hình thang.

BÀI 7: Hình thang có đáy lớn hơn đáy bé 20,4 dm và bởi 5/3 đáy bé, chiều cao hơn đáy bé nhỏ 2,1 dm. Tính diện tích s hình thang.

BÀI 8: Hình thang bao gồm tổng độ lâu năm hai đáy bởi 14,5 dm, đáy khủng gấp rưỡi đáy bé, chiều cao kém đáy bé nhỏ 2,8 dm. Tính diện tích hình thang.

BÀI 9: Hình thang gồm tổng độ dài hai đáy bằng 30,5 dm, lòng lớn bằng 1,5 lần đáy bé, độ cao hơn đáy bé xíu 6,2 dm. Tính diện tích hình thang.

BÀI 10: Hình thang tất cả tổng độ lâu năm hai đáy bằng 60 m, 1/3 đáy khủng bằng 50% đáy bé, độ cao bằng 80% lòng bé. Tính diện tích hình thang.

Bài 11: Tính diện tích hình thang biết:

a) Độ lâu năm hai lòng lần lượt là 12cm và 8cm; chiều cao là 5cm.

b) Độ nhiều năm hai đáy lần lượt là 9,4m cùng 6,6m; độ cao là 10,5m.

Bài 12: Một hình thang có đáy nhỏ dại dài 7cm, đáy phệ dài 17cm được phân thành hai hình thang tất cả đáy tầm thường dài 13cm. Hãy so sánh diện tích hai hình thang gồm đáy chung nói trên.