Toán hình 11 bài 5
Nội dung bài học sẽ giúp các em nắm được khái niệm, tính chất và các dạng bài tập liên quan đến Phép quay. Thông qua các ví dụ minh họa có hướng dẫn giải các em sẽ nắm được phương pháp làm bài, qua đó làm chủ nội dung bài học này.
Bạn đang xem: Toán hình 11 bài 5
1. Tóm tắt lý thuyết
1.1. Định nghĩa phép quay
1.2. Tính chất của phép quay
2. Bài tập minh hoạ
3.Luyện tập bài 5 chương 1 hình học 11
3.1 Trắc nghiệm về phép quay
3.2 Bài tập SGK và Nâng Cao về phép quay
4.Hỏi đáp vềbài 5 chương 1 hình học 11
a) Định nghĩa
Cho điểm O và góc lượng giác \(\alpha .\) Phép biến hình biến O thành chính nó và biến mỗi điểm M khác O thành M’ sao cho OM=OM’ và góc lượng giác (OM,OM’) bằng \(\alpha \) được họi là phép quay tâm O góc \(\alpha .\)
Ký hiệu: \({Q_{\left( {O,\alpha } \right)}}\)
- Điểm O gọi là tâm quay, \(\alpha \) gọi là góc quay.
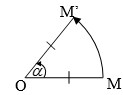
Nhận xét:
+ Chiều dương của phép quay là chiều dương của đường tròn lượng giác, ngược lại là chiều âm.
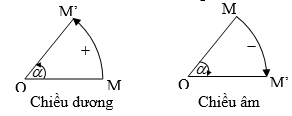
+ Với số nguyên k:
Phép quay \({Q_{\left( {O,k2\pi } \right)}}\) là phép đồng nhất.
Phép quay \({Q_{\left( {O,\pi + k2\pi } \right)}}\) là phép đối xứng tâm.
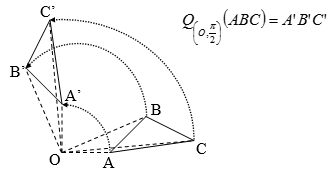
Cho tam giác ABC và điểm O. Hãy biểu diễn ảnh A’B’C’ của tam giác ABC qua phép quay tâm O góc quay \(\frac{\pi }{2}\).
1.2. Tính chất của phép quay
a) Tính chất 1
Phép quay bảo toàn khoảng cách giữa hai điểm bất kỳ.
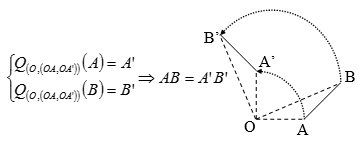
Phép quay biến đường thẳng thành đường thẳng, biến đoạn thẳng thành đoạn thẳng bằng nó, biến tam giác thành tam giác bằng nó, biến đường tròn thành đường tròn có cùng bán kính.
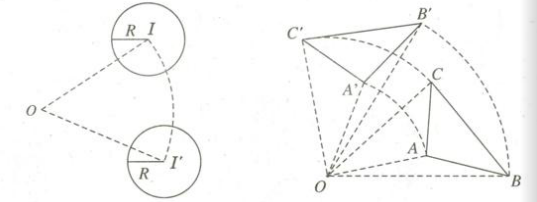
Phép quay góc quay \(0 Ví dụ 1:
Cho lục giác đều ABCDEF tâm O. Hãy xác định ảnh của:
a) \(\Delta OAB\) qua phép quay tâm O, góc quay 3600.
b) \(\Delta OAB\) qua phép quay tâm O, góc quay 1200.
c) \(\Delta OAB\) qua phép quay tâm O, góc quay -1800.
d) \(\Delta OAB\) qua phép quay tâm O, góc quay -3000.
Hướng dẫn giải: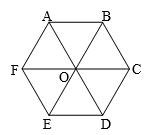
a) Ta có: \(\left\{ \begin{array}{l}{Q_{\left( {O{{,360}^0}} \right)}}\left( A \right) = A\\{Q_{\left( {O{{,360}^0}} \right)}}\left( B \right) = B\end{array} \right. \Rightarrow {Q_{\left( {O{{,360}^0}} \right)}}\left( {OAB} \right) = OAB\)
b) Ta có: \(\left\{ \begin{array}{l}{Q_{\left( {O{{,120}^0}} \right)}}\left( A \right) = E\\{Q_{\left( {O{{,120}^0}} \right)}}\left( B \right) = F\end{array} \right. \Rightarrow {Q_{\left( {O{{,120}^0}} \right)}}\left( {OAB} \right) = OEF.\)
c) Ta có: \(\left\{ \begin{array}{l}{Q_{\left( {O, - {{180}^0}} \right)}}\left( A \right) = D\\{Q_{\left( {O, - {{180}^0}} \right)}}\left( B \right) = E\end{array} \right. \Rightarrow {Q_{\left( {O, - {{180}^0}} \right)}}\left( {OAB} \right) = ODE.\)
d) Ta có: \(\left\{ \begin{array}{l}{Q_{\left( {O, - {{300}^0}} \right)}}\left( A \right) = F\\{Q_{\left( {O, - {{300}^0}} \right)}}\left( B \right) = A\end{array} \right. \Rightarrow {Q_{\left( {O, - {{300}^0}} \right)}}\left( {OAB} \right) = OFA.\)
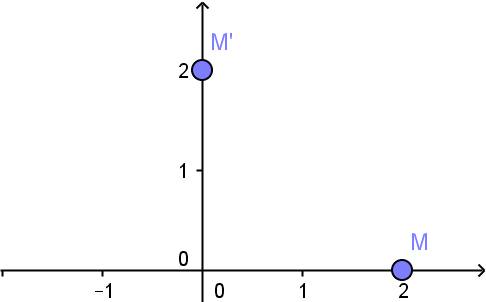
Ví dụ 2:Trong mặt phẳng Oxy cho điểm M(2;0) và đường thẳng d: \(x + 2y - 2 = 0,\) đường tròn \(\left( C \right):\) \({x^2} + {y^2} - 4x = 0.\) Xét phép quay Q tâm O góc quay \({90^0}.\)
a) Tìm ảnh của điểm M qua phép quay Q.
b) Tìm ảnh của d qua phép quay Q.
c) Tìm ảnh của (C) qua phép quay Q.
Hướng dẫn giải:a) Ta có: Vì \(M(2;0) \in Ox\) nên: \({Q_{\left( {0;{{90}^0}} \right)}}(M) = M":\left\{ \begin{array}{l}M" \in Oy\\OM = OM"\end{array} \right. \Rightarrow M"(0;2).\)
b) Ta có \(M\left( {2;0} \right) \in d,\) ảnh của M qua phép quay Q theo câu a là M’(0;2).
Gọi d’ là ảnh của d qua Q ta có d’ là đường thẳng qua M’ và vuông góc với d.
Đường thẳng d có VTPT là \(\overrightarrow n = \left( {1;2} \right),\) suy ra d’ có VTPT là \(\overrightarrow {n"} = \left( {2; - 1} \right)\)
Vậy phương trình của d’ là: \(2(x - 0) - 1(y - 2) = 0 \Leftrightarrow 2x - y + 2 = 0.\)
c) Đường tròn (C) có tâm M(2;0) và bán kính R=2.
Ảnh của M qua Q là M’(0;2).
Gọi (C) là ảnh của (C) qua Q, (C’) có tâm M’ và bán kính R=2.
Vậy phương trình của (C’) là: \({(x - 0)^2} + {(y - 2)^2} = 4.\)
Ví dụ 3:Tìm ảnh của điểm A(3;4) qua phép quay tâm O góc quay \({90^0}.\)
Hướng dẫn giải:Với phép quay tâm O góc 90 độ điểm A thành A’(x;y) có tọa độ thỏa mãn: \(\begin{array}{l}\left\{ \begin{array}{l}OA = OA"\\(OA;OA") = {90^0}\end{array} \right. \Rightarrow \left\{ \begin{array}{l}{3^2} + {4^2} = {x^2} + {y^2}\\\overrightarrow {OA} .\overrightarrow {OA"} = 0\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}{x^2} + {y^2} = 25\\3x + 4y = 0\end{array} \right. \Leftrightarrow \left< \begin{array}{l}\left\{ \begin{array}{l}x = - 4\\y = 3\end{array} \right.\\\left\{ \begin{array}{l}x = 4\\y = - 3\end{array} \right.\end{array} \right.\end{array}\)











