Tính diện tích hình bất kỳ
Ngoài hình vuông, hình chữ nhật, hình thoi, hình thang, còn vô số hình tứ giác khác mà bạn có lẽ sẽ cần phải tính diện tích. Ngoài các công thức thường thấy dành cho các hình tứ giác đặc biệt, liệu còn công thức nào để có thể tính diện tích hình tứ giác nào không? Hãy cùng tìm hiểu qua bài viết sau đây nhé! 1. Các hình tứ giác thường gặpTứ giác là hình có 4 đỉnh và 4 cạnh và đặc điểm nhận ra đó là không có bất kì 2 đoạn thẳng nào cùng nằm trên một đường thẳng. Hình tứ giác có 4 góc, và tổng số đo 4 góc trong tứ giác = 360 độ.Bạn đang xem: Công thức tính diện tích tứ giác bất kỳ Có hai loại tứ giác là tứ giác lồi và tứ giác lõm. Các dạng tứ giác lồi cơ bản thường gặp: Hình thoi, hình thang, hình bình hành, hình chữ nhật, hình vuông, tứ giác nội tiếp, tứ giác ngoại tiếp, Với tứ giác lõm (hay còn gọi là tứ giác không lồi), một góc trong có số đo lớn hơn 180° và một trong hai đường chéo nằm bên ngoài tứ giác. Bạn đang xem: Tính diện tích hình bất kỳ 2. Các công thức tính diện tích hình tứ giácCông thức chung để áp dụng tính bất cứ diện tích hình tứ giác nào như sau: 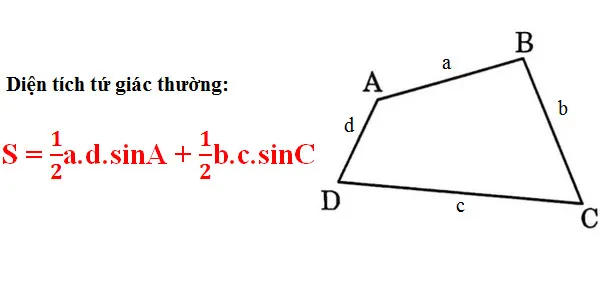 Như vậy, để tính diện tích tứ giác bất kỳ không thuộc 1 trong cách hình trên, bạn cần tìm độ dài của 4 cạnh (giả sử a, b, c, d, trong đó a và c, b và d là các cạnh đối diện nhau). Sau đó đi tính 2 góc đối diện. Ngoài ra, công thức tính diện tích hình tứ giác phổ biến và thường thấy trong các bài tập như sau: + Hình vuông:Là tứ giác lồi có 4 cạnh bằng nhau và 4 góc vuông. S = a x a Trong đó:S: Diện tích hình vuônga: Độ dài cạnh + Hình chữ nhật:Là tứ giác lồi có 2 cặp cạnh đối diện bằng nhau và 4 góc vuông. S = a x b Trong đó:S: Diện tích hình chữ nhậta: Chiều dàib: Chiều rộng + Hình bình hành:Là tứ giác lồi có hai cặp cạnh đối diện song song và bằng nhau. S = a x h Trong đó:S: Diện tích hình bình hànha: Cạnh đáy hình thoih: Đường cao hình thoi S = 12 (d1 x d2) Trong đó:S: Diện tích hình thoid1, d2: Độ dài 2 đường chéo Bạn cũng có thể tính diện tích hình thoi theo cách tính diện tích hình bình hành. + Hình thang:Là tứ giác lồi có 1 cặp cạnh song song. S = 12 (a+b) x h Trong đó:S: Diện tích hình thanga,b: Độ dài 2 cạnh song songh: Chiều cao Khi tứ giác thuộc hình bất kì, không thuộc các hình đã kiệt kê ở trên và có độ dài các cạnh khác nhau, không có cặp cạnh nào song song với nhau, ta có thể áp dụng công thức Brahmagupta: 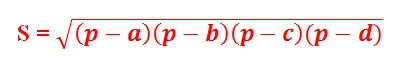 Bốn cạnh của tứ giác lần lượt là a, b, c, d trong đó cạnh a đối diện với cạnh c, cạnh b đối diện với cạnh d. Trong đó, P là nửa chu vi của tứ giác, và P = (a + b + c + d)/2 Nếu biết trước 4 cạnh và hai đường chéo m, n của hình tứ giác bất kỳ, bạn cũng có thể sử dụng công thức như sau: S = /2 Trong đó B chính là góc được tạo bởi hai đường chéo của tứ giác 3. Bài tập áp dụngBài 1: Cho tứ giác ABCD, có cạnh AB = 3cm, cạnh BC = 5cm, cạnh CD = 2cm, cạnh DA = 6cm. Cho góc A = 110 độ, góc C = 80 độ. Tính diện tích tứ giác ABCD. Bài giải: Theo công thức tính diện tích tứ giác, S = 0,5 a.d.sinA + 0,5.b.c.sinC=> Diện tích tứ giác ABCD là S = 0,5.3.6.sin110 + 0,5.5.2.sin 80 = 9.0,939 + 5.0,984 = 8,451 + 4,92 = 13,371 cm2Vậy diện tích của tứ giác ABCD bằng13,371cm2 Bài 2: Cho tứ giác nội tiếp ABCD, có cạnh AB = 3cm, cạnh BC = 5cm, cạnh CD = 2cm, cạnh DA = 6cm. Tính diện tích tứ giác ABCD. nửa chu vi của tứ giác là: P = 8 cm Ta áp dụng công thức Brahmagupta vào để tính diện tích hình tứ giác. Và kết quả S = 13,4cm2. Xem thêm: Hướng Dẫn 2 Cách Lấy Lại Mật Khẩu Gmail Không Cần Số Điện Thoại Trên đây là bao quát về các công thức và cách tính diện tích hình tứ giác nói chung, bất kể đó là hình đặc biệt hay hình tứ giác thông thường. Tùy vào dữ kiện đề bài mà có thể bạn sẽ cần triển khai các bước khác nhau để tìm được giá trị diện tích chuẩn nhất.Chuyên mục: Ngoài hình vuông, hình chữ nhật, hình thoi, hình thang, còn vô số hình tứ giác khác mà bạn có lẽ sẽ cần phải tính diện tích. Ngoài các công thức thường thấy dành cho các hình tứ giác đặc biệt, liệu còn công thức nào để có thể tính diện tích hình tứ giác nào không? Hãy cùng tìm hiểu qua bài viết sau đây nhé! 1. Các hình tứ giác thường gặpTứ giác là hình có 4 đỉnh và 4 cạnh và đặc điểm nhận ra đó là không có bất kì 2 đoạn thẳng nào cùng nằm trên một đường thẳng. Hình tứ giác có 4 góc, và tổng số đo 4 góc trong tứ giác = 360 độ.Bạn đang xem: Công thức tính diện tích tứ giác bất kỳ Có hai loại tứ giác là tứ giác lồi và tứ giác lõm. Các dạng tứ giác lồi cơ bản thường gặp: Hình thoi, hình thang, hình bình hành, hình chữ nhật, hình vuông, tứ giác nội tiếp, tứ giác ngoại tiếp, Với tứ giác lõm (hay còn gọi là tứ giác không lồi), một góc trong có số đo lớn hơn 180° và một trong hai đường chéo nằm bên ngoài tứ giác. 2. Các công thức tính diện tích hình tứ giácCông thức chung để áp dụng tính bất cứ diện tích hình tứ giác nào như sau:  Như vậy, để tính diện tích tứ giác bất kỳ không thuộc 1 trong cách hình trên, bạn cần tìm độ dài của 4 cạnh (giả sử a, b, c, d, trong đó a và c, b và d là các cạnh đối diện nhau). Sau đó đi tính 2 góc đối diện. Ngoài ra, công thức tính diện tích hình tứ giác phổ biến và thường thấy trong các bài tập như sau: + Hình vuông:Là tứ giác lồi có 4 cạnh bằng nhau và 4 góc vuông. S = a x a Trong đó:S: Diện tích hình vuônga: Độ dài cạnh + Hình chữ nhật:Là tứ giác lồi có 2 cặp cạnh đối diện bằng nhau và 4 góc vuông. S = a x b Trong đó:S: Diện tích hình chữ nhậta: Chiều dàib: Chiều rộng + Hình bình hành:Là tứ giác lồi có hai cặp cạnh đối diện song song và bằng nhau. S = a x h Trong đó:S: Diện tích hình bình hànha: Cạnh đáy hình thoih: Đường cao hình thoi S = 12 (d1 x d2) Trong đó:S: Diện tích hình thoid1, d2: Độ dài 2 đường chéo Bạn cũng có thể tính diện tích hình thoi theo cách tính diện tích hình bình hành. + Hình thang:Là tứ giác lồi có 1 cặp cạnh song song. S = 12 (a+b) x h Trong đó:S: Diện tích hình thanga,b: Độ dài 2 cạnh song songh: Chiều cao Khi tứ giác thuộc hình bất kì, không thuộc các hình đã kiệt kê ở trên và có độ dài các cạnh khác nhau, không có cặp cạnh nào song song với nhau, ta có thể áp dụng công thức Brahmagupta:  Bốn cạnh của tứ giác lần lượt là a, b, c, d trong đó cạnh a đối diện với cạnh c, cạnh b đối diện với cạnh d. Trong đó, P là nửa chu vi của tứ giác, và P = (a + b + c + d)/2 Nếu biết trước 4 cạnh và hai đường chéo m, n của hình tứ giác bất kỳ, bạn cũng có thể sử dụng công thức như sau: S = /2 Trong đó B chính là góc được tạo bởi hai đường chéo của tứ giác 3. Bài tập áp dụngBài 1: Cho tứ giác ABCD, có cạnh AB = 3cm, cạnh BC = 5cm, cạnh CD = 2cm, cạnh DA = 6cm. Cho góc A = 110 độ, góc C = 80 độ. Tính diện tích tứ giác ABCD. Bài giải: Theo công thức tính diện tích tứ giác, S = 0,5 a.d.sinA + 0,5.b.c.sinC=> Diện tích tứ giác ABCD là S = 0,5.3.6.sin110 + 0,5.5.2.sin 80 = 9.0,939 + 5.0,984 = 8,451 + 4,92 = 13,371 cm2Vậy diện tích của tứ giác ABCD bằng13,371cm2 Bài 2: Cho tứ giác nội tiếp ABCD, có cạnh AB = 3cm, cạnh BC = 5cm, cạnh CD = 2cm, cạnh DA = 6cm. Tính diện tích tứ giác ABCD. nửa chu vi của tứ giác là: P = 8 cm Ta áp dụng công thức Brahmagupta vào để tính diện tích hình tứ giác. Và kết quả S = 13,4cm2. Trên đây là bao quát về các công thức và cách tính diện tích hình tứ giác nói chung, bất kể đó là hình đặc biệt hay hình tứ giác thông thường. Tùy vào dữ kiện đề bài mà có thể bạn sẽ cần triển khai các bước khác nhau để tìm được giá trị diện tích chuẩn nhất.Chuyên mục: |











