Định nghĩa, tính chất, dấu hiệu nhận biết của hình chữ nhật
Trong nội dung bài viết dưới đây, điện máy letspro.edu.vn sẽ chia sẻ tới chúng ta lý thuyết hình chữ nhật là gì? vệt hiệu nhận thấy và đặc thù hình chữ nhật kèm theo các dạng bài tập về hình chữ nhật bao gồm lời giải cụ thể giúp bạn khối hệ thống lại loài kiến thức của chính bản thân mình để vận dụng vào làm bài tập nhé
Hình chữ nhật là gì?
Hình chữ nhật là một hình tứ giác gồm bốn góc vuông.
Bạn đang xem: Định nghĩa, tính chất, dấu hiệu nhận biết của hình chữ nhật
Ví dụ: Tứ giác ABCD là hình chữ nhật khi còn chỉ khi ABCD là tứ giác gồm Aˆ = Bˆ = Cˆ = Dˆ = 900
Nhận xét: Hình chữ nhật cũng là 1 trong hình bình hành cũng là 1 hình thang cân
Tính hóa học hình chữ nhật
Trong một hình chữ nhật có:
Trong hình chữ nhật, hai đường chéo bằng nhau và cắt nhau tại trung điểm của mỗi đường.Có tất cả các đặc điểm của hình thang cân nặng và hình bình hành.Các đường chéo cánh cắt nhau tạo thành 4 tam giác cân.Trong tam giác vuông, mặt đường trung tuyến đường ứng với cạnh huyền thì bằng nửa cạnh huyền.Dấu hiệu nhận ra hình chữ nhật
Tứ giác có cha góc vuông là hình chữ nhật.Hình thang cân gồm một góc vuông là hình chữ nhật.Hình bình hành có một góc vuông là hình chữ nhật.Hình bình hành tất cả hai đường chéo cánh bằng nhau là hình chữ nhật.Bài tập về cách minh chứng hình chữ nhật
Dạng 1: chứng tỏ tứ giác là hình chữ nhật
Phương pháp giải: Vận dụng các dấu hiệu phân biệt để chứng minh một tứ giác là hình chữ nhật.
Tứ giác có cha góc vuông là hình chữ nhật.Hình thang cân bao gồm một góc vuông là hình chữ nhật.Hình bình hành gồm một góc vuông là hình chữ nhật.Hình bình hành gồm hai đường chéo cánh bằng nhau là hình chữ nhật.Ví dụ 1: mang đến tam giác ABC vuông trên A, điểm M bất kì trên cạnh BC. Call D với E theo đồ vật tự là chân mặt đường vuông góc kẻ tự M mang đến AB và AC. Tứ giác ADME là hình gì? trên sao?
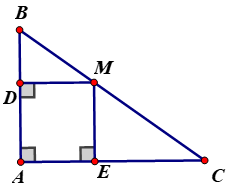
Lời giải
ΔABC vuông tại A đề xuất BACˆ = 900; nhưng mà D nằm trong cạnh AB, E trực thuộc cạnh AC đề xuất DAEˆ = 900
Vì MD ⊥ AB tại D nên ADMˆ = 900
ME ⊥ AC tại E bắt buộc AEMˆ = 900
Xét tứ giác ADME có:
DAEˆ = ADMˆ = AEMˆ = 900
Vậy tứ giác ADME là hình chữ nhật (theo tín hiệu nhận biết).
Ví dụ 2: mang đến tam giác ABC cân nặng tại A, các đường trung con đường BM, CN cắt nhau trên G. Gọi D là điểm đối xứng cùng với G qua M, gọi E là điểm đối xứng với G qua N. Tứ giác BEDC là hình gì? vị sao?
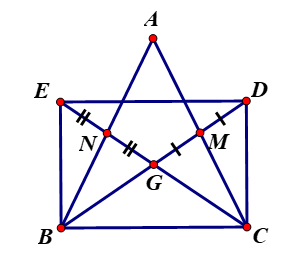
Lời giải
Ta có hai tuyến phố trung tuyến BM cùng CN giảm nhau tại G đề xuất G là trung tâm tam giác ABC.
Theo đặc điểm trọng trọng điểm tam giác ta có:
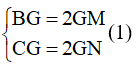
Lại có: G đối xứng cùng với với D qua M => GM = MD GD = 2GM (2)
G đối xứng với E qua N => GN = EN => GE = 2GN (3)
Từ (1); (2); (3) =>
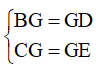
Xét tứ giác BCDE có:
G là trung điểm của đường chéo BD
G là trung điểm đường chéo cánh CE
Do đó: tứ giác BCDE là hình bình hành
Lại có:
ΔABC cân tại A nên AB = AC. Nhưng mà M là trung điểm của AC, N là trung điểm AB buộc phải BN = CM
Xét tam giác BNC với tam giác CMB có:
BC chung
BN = CM
NBCˆ = MCBˆ (do tam giác ABC cân nặng tại A)
Do đó: ΔBNC = ΔCMB (c – g –c)
=> công nhân = BM (hai cạnh tương ứng)
Mà
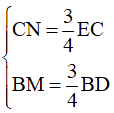
Do kia EC = BD.
Xét hình bình hành BCDE có hai tuyến đường chép EC và BD bằng nhau
=> Hình bình hành BCDE là hình chữ nhật (dấu hiệu thừa nhận biết).
Dạng 2: Vận dụng đặc điểm hình chữ nhật để chứng tỏ các đặc thù hình học
Phương pháp giải: áp dụng định nghĩa và các tính chất về cạnh, góc và đường chéo của hình chữ nhật và các kiến thức vẫn học về tứ giác đặc biệt.
Ví dụ 1: Tứ giác ABCD bao gồm AB ⊥ CD. Gọi E, F, G, H theo thiết bị tự là trung điểm của BC, BD, AD, AC. Chứng tỏ rằng EG = FH.
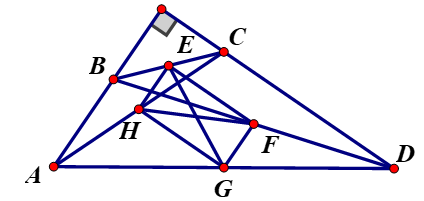
Vì E là trung điểm của BC, H là trung điểm của AC cần EH là đường trung bình của ΔABC => EH // AB (*) cùng EH = ½ AB (tính hóa học đường vừa đủ của tam giác) (1)
Tương từ bỏ ta minh chứng được GF là con đường trung bình của ΔABD => GF // AB cùng GF = ½ AB (tính hóa học đường trung bình của tam giác) (2)
Từ (1) cùng (2) => HE // GF; HE = GF => GHEF là hình bình hành (theo tín hiệu nhận biết) (**)
Mặt khác ta cũng chứng minh được EF là mặt đường trung bình của ΔBCD => EF // CD (3)
Kết phù hợp với AB ⊥ CD (gt) (4)
Kết hợp (*), (3) và (4) => HE ⊥ EF => HEFˆ = 900 (***)
Từ (**) và (***) ta bao gồm EFGH là hình chữ nhật (theo dấu hiệu nhận biết). Từ đó suy ra hai đường chéo EG = FH (tính hóa học của hình chữ nhật).
Xem thêm: Những Trường Hợp Bị Nghi Là Du Hành Vượt Thời Gian Trên Thế Giới
Ví dụ 2:Cho hình chữ nhật ABCD. Rước điểm p. Tùy ý trên đường chéo BD. Gọi M là điểm đối xứng của C qua P.
a. Chứng tỏ AM // BD
b. Hotline E, F theo thứ tự là hình chiếu của M trên AD, AB. Minh chứng AEMF là hình chữ nhật
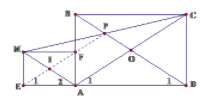
Lời giải
a. Gọi O là giao điểm của BD và AC
Ta gồm OP là con đường trung bình của ΔAMC ⇒ OP // AM
b, Xét tứ giác AEMF gồm Eˆ = Aˆ = Fˆ = 900 ⇒ AEMF là hình chữ nhật
Dạng 3: áp dụng định lý thuận và đảo của con đường trung tuyến ứng cùng với cạnh huyền của tam giác vuông
Phương pháp giải: thực hiện định lý về đặc thù đường trung con đường ứng với cạnh huyền của tam giác vuông để tính độ nhiều năm đoạn thẳng hoặc minh chứng các hình cân nhau hoặc minh chứng tam giác vuông.
Ví dụ 1: mang đến hình chữ nhật ABCD. Gọi H là chân mặt đường vuông góc kẻ từ A đến BD. Biết HB = 2 cm, HD = 6 cm. Tính độ dài AB, AD.
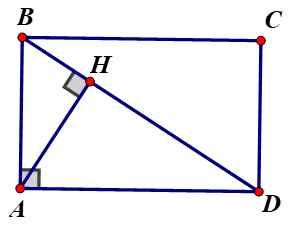
Lời giải
Ta có: BD = HB + HD = 2 + 6 = 8 cm.
Xét tam giác giác BHA vuông tại H ta có:
BH2 + AH2 = AB2 (định lý Py – ta – go)
⇔ AH2 = AB2 – BH2
⇔ AH2 = AB2 – 22
⇔ AH2 = AB2 – 4 (1)
Xét tam giác AHD vuông tại H ta có:
HD2 + AH2 = AD2 (định lý Py – ta – go)
⇔ AH2 = AD2 – HD2
⇔ AH2 = AD2 – 62
⇔ AH2 = AD2 – 36 (2)
Từ (1); (2) => AB2 – 4 = AD2 – 36 (3)
Xét tam giác ABD vuông trên A có:
AB2 + AD2 = DB2 (định lý Py – ta – go)
AB2 + AD2 = 82
⇔ AB2 = 64 – AD2 vậy vào (3)
⇔ 64 – AD2 – 4 = AD2 – 36
⇔ 2AD2 = 96
⇔ AD2 = 48
⇔ AD = 4√3
=> AB2 = 64 – (4√3)2
⇔ AB2 = 16
=> AB = 4 cm
Vậy AD = 4√3 ; AB = 4 cm
Dạng 4. Tìm điều kiện để tứ giác là hình chữ nhật
Phương pháp giải: áp dụng định nghĩa, tính chất, lốt hiệu nhận biết hình chữ nhật.
Ví dụ: mang lại tứ giác ABCD. điện thoại tư vấn E, F, G, H theo trang bị tự là trung điểm của các cạnh AB, BC, CD, DA.
a) minh chứng EFGH là hình bình hành.
b) Tìm đk của tứ giác ABCD nhằm EFGH là hình chữ nhật.
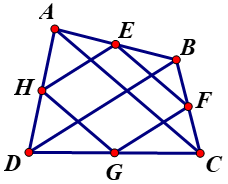
Lời giải
a) Ta có:
E là trung điểm của AB, H là trung điểm của AD đề xuất HE là con đường trung bình của ΔABD
⇒ HE // BD; HE = ½BD (1)
F là trung điểm BC, G là trung điểm của DC bắt buộc FG là con đường trung bình của ΔBCD nên:
⇒ FG // BD; FG = ½BD (2)
Từ (1) cùng (2)
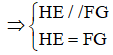
Xét tứ giác EFGH ta có
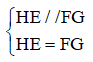
Do đó: EFGH là hình bình hành (theo dấu hiệu nhận biết)
b) giả sử EFGH là hình chữ nhật ⇒ HEFˆ = 900 ⇔ HE ⊥ EF (3)
Ta có:
E là trung điểm của AB,
F là trung điểm của BC
Do đó: EF là con đường trung bình của
=> EF //AC (tính hóa học đường mức độ vừa phải của tam giác) (4)
Mà HE // BD (chứng minh a) (5)
Từ (3), (4), (5) => BD ⊥ AC .
=> Tứ giác ABCD có 2 đường chéo vuông góc.
Tứ giác ABCD cần phải có thêm đk hai đường chéo vuông góc thì EFGH là hình chữ nhật.
Bên trên chính là toàn cỗ định nghĩa, vết hiệu nhận ra và đặc thù hình chữ nhật hoàn toàn có thể giúp chúng ta áp dụng để minh chứng tứ giác là hình chữ nhật đối chọi giản
