Home / Bạn Quan Tâm / lý thuyết hệ hai phương trình bậc nhất hai ẩn

Lý thuyết hệ hai phương trình bậc nhất hai ẩn

admin 10/05/2023

Xin chào tất cả các bạn, hôm này mình sẽ hướng dẫn cho các bạn 5 cách giải hệ hai phương trình bậc nhất hai ẩn, nắm được 5 phương pháp này thì bạn sẽ không phải “ngại” bất kỳ trường hợp nào cả.

Bạn đang xem: Lý thuyết hệ hai phương trình bậc nhất hai ẩn

Cụ thể thì chúng ta sẽ có: Phương pháp cộng, phương pháp thế, phương pháp đồ thị, phương pháp cao cấp (ma trận nghịch đảo, định thức) và phương pháp sử dụng máy tính CASIO.

Trong đó, 3 phương pháp đầu tiên là dành cho học sinh Trung học, phương pháp thứ tư dành cho sinh viên, còn riêng phương pháp sử dụng máy tính CASIO mang tính chất hỗ trợ, kiểm tra kết quả là chính.

Mục Lục Nội Dung

I. Định nghĩa về hệ hai phương trình bậc nhất hai ẩn

Hệ hai phương trình bậc nhất 2 ẩn có dạng $\left\{\begin{array}{ll}ax+by&=c \\ a’x+b’y&=c’\end{array}\right.$

$x, y$ là 2 ẩn$a, b, c, a’, b’, c’$ là các số thực.

Chẳng hạn $\left\{\begin{array}{ll}2x+y&=4 \\ x-y&=-1\end{array}\right.$ là hệ hai phương trình bậc nhất hai ẩn

#1. Sử dụng phương pháp cộng

Phương pháp này nên sử dụng khi hệ phương trình có $a+a’=0$ hoặc $b+b’=0$

Quan sát hệ phương trình đã cho ta thấy $b+b’=0$ cụ thể $1+(-1)=0$

Lời Giải:

$\left\{\begin{array}{ll}2x+y&=4 \\ x-y&=-1\end{array}\right.$

$\Leftrightarrow \left\{\begin{array}{ll}3x&=3 \\ x-y&=-1\end{array}\right. \Leftrightarrow \left\{\begin{array}{ll}x&=1 \\ x-y&=-1\end{array}\right. \Leftrightarrow \left\{\begin{array}{ll}x&=1 \\ 1-y&=-1\end{array}\right. \Leftrightarrow \left\{\begin{array}{ll}x&=1 \\ y&=2\end{array}\right.$

Vậy nghiệm của hệ phương trình đã cho là (1; 2)

#2. Phương pháp thế

Phương trình có hệ số càng đơn giản thì lúc biểu diễn x theo y hoặc y theo x sẽ càng dễ dàngẨn nào có hệ số bằng 1 thì ưu tiên biểu diễn ẩn đó theo ẩn còn lại

Đối với hệ phương trình này mình sẽ chọn phương trình thứ nhì $x-y=-1$ và biểu diễn x theo y

Lời Giải:

$\left\{\begin{array}{ll}2x+y&=4 \\ x-y&=-1\end{array}\right.$

$\Leftrightarrow \left\{\begin{array}{ll}2x+y&=4 \\ x&=-1+y\end{array}\right. \Leftrightarrow \left\{\begin{array}{ll}2(-1+y)+y&=4 \\ x&=-1+y\end{array}\right. \Leftrightarrow \left\{\begin{array}{ll}y&=2 \\ x&=-1+y\end{array}\right. \Leftrightarrow \left\{\begin{array}{ll}y&=2 \\ x&=1 \end{array}\right.$

=> Vậy nghiệm của hệ phương trình đã cho là (1; 2)

#3. Phương pháp đồ thị

Phương pháp đồ thị chỉ nên sử dụng khi các hệ số là những số nguyên nha các bạn.

Xem thêm: Nhạc Hay Dành Cho Bà Bầu 0, Nhạc Tuyển Chọn Cho Bà Bầu Và Thai Nhi

Lời Giải:

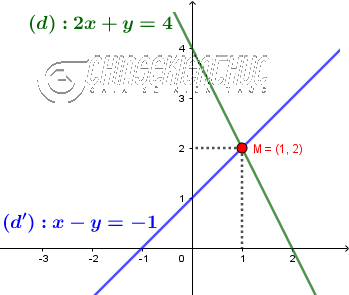
Gọi hai đường thẳng xác định bởi hai phương trình trong hệ đã cho lần lượt là $(d): 2x+y=4$ và $(d’): x-y=-1$

Vẽ (d) và (d’) trên cùng một hệ trục tọa độ ta thấy chúng cắt nhau tại một điểm $M=(1; 2)$ duy nhất.

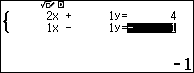Có thể bạn sẽ thích?Cách giải hệ phương trình bằng máy tính CASIO (FX 580 VNX và 880BTG)

II. Lời kết

Okay, trên đây là 5 phương pháp giải hệ hai phương trình bậc nhất hai ẩn mà mình đã tổng hợp lại.

Tùy thuộc vào hệ phương trình cụ thể mà chúng ta sẽ cân nhắc lựa chọn phương pháp cho phù hợp nhất.

Phương pháp cộng và phương pháp thế là 2 phương pháp bạn nên ưu tiên sử dụng.Phương pháp đồ thị sử dụng khá hạn chế vì phương pháp này chỉ khả dụng khi nghiệm có giá trị nguyên.Phương pháp cao cấp chỉ sử dụng được khi hệ phương trình có nghiệm duy nhất.Còn phương pháp sử dụng máy tính CASIO chỉ nên sử dụng để kiểm tra lại kết quả.